 |

4.1 Binary numbers
Computers can only work with zero and one values, in the binary
numeric system. You can say they're pretty stupid, but they are so fast
that, to most people, they look like very smart devices. You probably wonder
how you get to see all those wonderfull stuff on your computer's display, if
it only knows ones and zeros. How all the books, games, movies, music and everything,
how all of these are stored only with 0 and 1 values? Well, if you pay a little
attention to this chapter, you will learn that.
Think on how, with only ten digits, from 0 to 9, you can write pretty big numbers.
The same way you can write more than two numbers with only 0 and 1 digits. In
fact, you can count as many numbers with 0 and 1 digits, as you can count with
0 to 9. Here is a go:
| decimal | binary |
| 0 | 0 |
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
|
| decimal | binary |
| 8 | 1000 |
| 9 | 1001 |
| 10 | 1010 |
| 11 | 1011 |
| 12 | 1100 |
| 13 | 1101 |
| 14 | 1110 |
| 15 | 1111 |
|
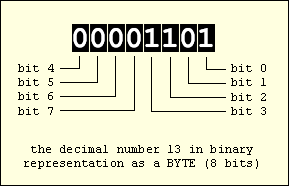
|
The digits of a binary number are called bits and they are counted from right
to left, starting with position 0. So, as may bits a binary number has, the
bigger it is. Of course 0110 is the same as 110 because, like for decimal numbers, the leading zeros can be ignored.
As you can see above, the number 7 needs 3 bits to be represented
in binary format. And if you continue the counting, by the time you reach the
number 255, you will be using 8 bits to represent it, all set to 1 (255 = 11111111).
That is called one BYTE. And since we are here, 1024 BYTES (not 1000) are called
one KILOBYTE, 1024 KILOBYTES are one MEGABYTE and so one. If you already know
this stuff, you probably got bored already, so let's go one with our programming
language.

The integer values accepted in GS9 programing language are using 32 bits to
represent numbers, and that is quite enough.
You can write the integer values in their binary form using the 0b
prefix in front of the binary number.
If you think at the bits as black (0) and white (1) points on the screen, you
will get an idea about how such an image is represented in the computer.
More detailed info on binary numbers you can get from
internet.
4.2 Hexadecimal numbers
Another numeric system used by programming languages is the hexadecimal system.
It uses the digits from 0 to 9 and another six, from A to F coresponding to 10
to 15 in decimal. It's like having 16 fingers :) So counting in hexadecimal is
0, 1, ..., 9, A, B, C, D, E, F, 10, 11, 12, ..., 19, 1A, 1B, ..., 1F, 20, 21, ... etc.

In GS9 you can write the integer values in their hexadecimal form using the 0x
prefix in front of the hexadecimal number.
Hexadecimal numbers can be used to represent color data in a friendly way. Computer
colors are composed from three color channels: red, green and blue. Each of these
channels can have up to 256 levels (values from 0x00 to 0xff).
For black we have all channels at minimnum (red=0, green=0, blue=0).
For white we have all channels at maximum (red=0xff, green=0xff, blue=0xff).
Sometimes, a forth channel, named alpha, is used to specify the transparence level (0x00=invisible, 0xff=opaque).
The hexadecimal format allows us
to write those values grouped in a single number, like 0x000000 for black and
0xffffff for white.
A full red is 0xff0000,
a full green is 0x00ff00 and
a full blue is 0x0000ff.
By having various values in these three channels, we can have
up to 16 million colors.
Such data values are used to represent the pixels from
the screen and storing lines of such pixels, we can store colored images. And
at last, storing multiple images, we can have animations and movies.
More detailed info on hexadecimal numbers you can get from the
internet.
4.3 ASCII characters
By the ASCII convention, each character from a
standard computer alphabet has a number associated to it. There are 256 ASCII
characters (from 0 to 255), but only some of them are printable. For example the
number 97 is associated to the character "a" and 98 is associated to "b".
But the ASCII characters are not only alphabetic characters. They also include
numbers like 0, 1, 2, 8, 9 or characters like +, -, #, !, (, ) etc.

In GS9, you can write integer numbers using the coresponding ASCII character in aphostrophes ' '
This is a way to store texts, emails or even whole books, using integer numbers. And since integer numbers are
represented inside the computer in binary format, even this text, you are reading right now, is stored as 0 and 1.
You can learn more about ASCII codes on
internet.

Here you can see a list of all numbers from 0 to 255 in decimal, hexadecimal and binary formats,
including their printable ASCII characters (for numbers between 32 and 126).
Now, we are ready to move on and see what can we do with all these data values and variables.
|
 |